[强化学习][python] 在 tic-tac-toe 上实现 蒙特卡洛搜索树 MCTS 算法

前置知识 UCB

强化学习的核心问题之一是 探索&利用 问题。最简单的解决方法是 $\epsilon-greedy$ 。 UCB是比 $\epsilon-greedy$ 稍微复杂一点的方法，对于UCB而言，其选择下一个动作的方式为：

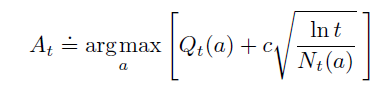
注意到，不同于 $\epsilon-greedy$ 会产生一个概率分布，然后用 np.random.choice 从其中sample一个动作；UCB是determinstic的，每次选择的动作都是确定的。

观察上式，可以分为两部分：

• exploitation：$argmax_a{Q_t(a)}$ 就是贪心算法。
• exploration：$c \sqrt{\frac{\ln t}{N_t(a)}}$ 用于衡量动作 $a$ 的 $Q$值的不确定性。 （ c是超参，一般选 $\sqrt2$，t是iteration次数，$N_t(a)$ 是t时刻动作a被选中的次数）。

可以这么理解 $c \sqrt{\frac{\ln t}{N_t(a)}}$ ： 它衡量了 $Q_t(a)$ 的不确定性， 当 $N_t(a)$ 趋向于无穷大时，根据大数定律，$Q_t(a)$ 是准确的， 所以此时$c \sqrt{\frac{\ln t}{N_t(a)}}$也正好趋向于0。详细的解释可以参看 https://zhuanlan.zhihu.com/p/32356077

例子

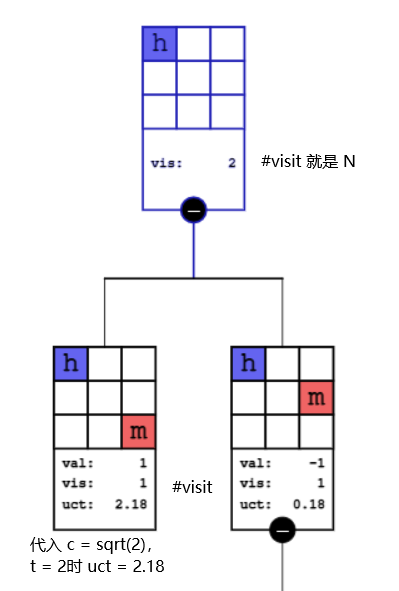
(来源：tic-tac-toe MCTS可视化 强烈推荐)

以tic-tac-toe为例，人（下图中的h）走先手。

对于左子结点，$ucb = Q_t(a) + c \sqrt{\frac{\ln t}{N_t(a)}} = 1 + \sqrt2 \sqrt{\frac{\ln 2}{1}} \approx 2.18$

对于右子结点而言，$ucb = Q_t(a) + c \sqrt{\frac{\ln t}{N_t(a)}} = -1 + \sqrt2 \sqrt{\frac{\ln 2}{1}} \approx 0.18$

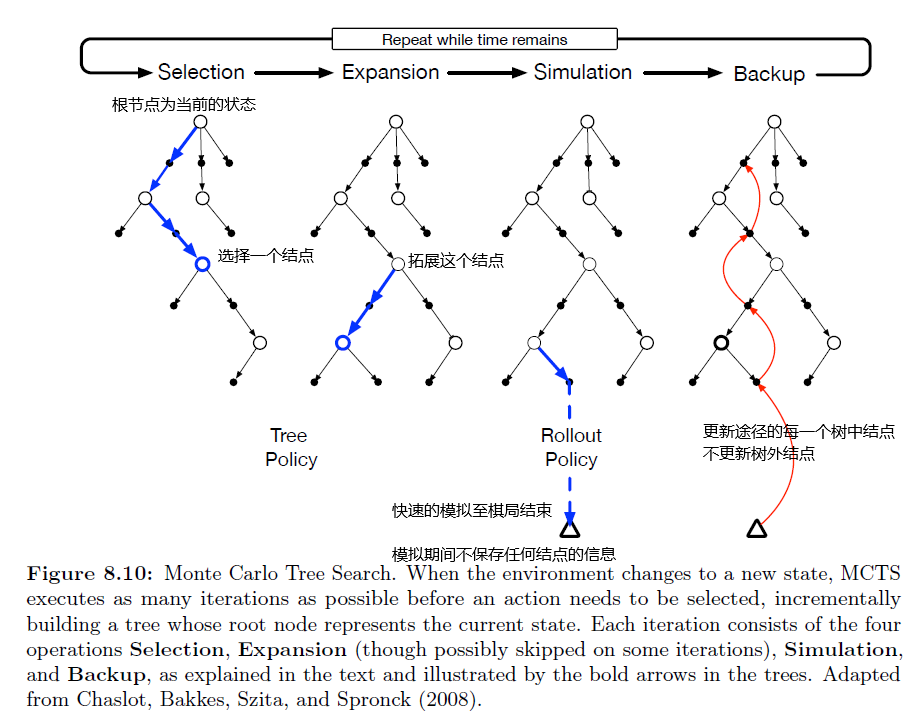
MCTS算法

MCTS分为 selection，expansion，simulation，backup。

我在tic-tac-toe上实现了MCTS，该实现参考了A Survey of Monte Carlo Tree Search Methods 中的算法，代码见 github (仍在整理中) 。

在开始叙述MCTS算法之前，先明确几点:

• MCTS是一个 Decision-time Planning, Rollout Algorithm。这代表 MCTS在遇到每个state之后，为该state做多趟蒙特卡洛模拟，估计出各个action的state-value（即 $Q$） 值之后，选择某个动作，然后丢弃刚学到的所有 state-value值。
• MCTS的数据结构是一颗树，树的每一个结点是一个state，边代表动作，子结点是父结点的afterstate，根结点是智能体当前所处的state。
• 对于井字棋，$Q$ 的意义是选择这个action之后，赢的平均概率。

Selection

selection：通过Tree-Policy从树中选择一个结点进行expansion。

这里的Tree-Policy选择的是前置知识中的UCB：

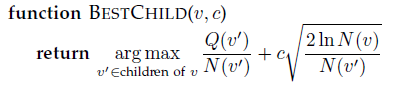
（这里的 $Q$ 指的是累计奖赏，不是平均奖赏，不过区别不大）

例子

在下图中，人走了第一步，现在agent需要做MCTS走第二步。

在第11次蒙特卡洛时，由于根结点Fully Expanded了，所以选择UCB最大的，即第一个子结点。该子结点是not fully expanded的，所以选择该子结点（下图中红色的结点）

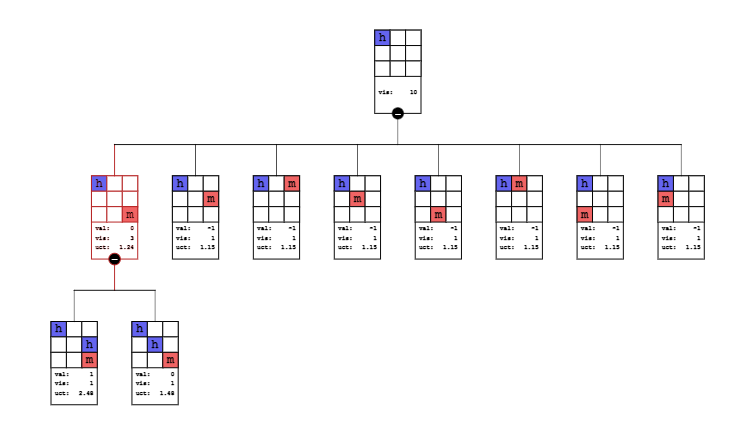
Expansion

Expansion：对于selection选中的结点，生成它的一个子结点，如果有多个可能子结点，随机选择一个。

（这一步没什么好说的，单纯的new一个结点）

Simulation

Simulation：以生成的子结点 $v^{\prime}$ 为起点，利用Rollout Policy（也叫 Default Policy）选择动作，并进入下一个结点，直到达到终止状态，得到reward。对于tic-tac-toe，reward为 -1，0，1。

• Simulation 与 Selection都用了Policy，但是Simulation使用的是 更简单的Policy，比如均匀随机选择一个动作。

Backup

Backup: 从根结点到新生成的结点，在树中形成了一条路径。 backup所做的，就是利用simulation得到的reward，更新这条路径上的所有结点（包括根结点和新结点）。

需要更新的有：

• $N(v)$：状态 $v$ 被backup的总次数。
• $Q(v)$：从 $v$ 出发，获得的累计总奖赏。

这里特别注意的是，对于tic-tac-toe这种两人游戏，假设根结点处在第1层，那么奇数层是站在智能体的角度，偶数层站在对手的角度。当站在智能体的角度，reward不需要修改；当站在对手的角度，reward = - reward。这里实现的时候要小心。

决策

在利用蒙特卡洛模拟学习出了 $Q$ 之后，接着要选择一个动作，选择的方式可以有很多种，这里还是根据UCB的值来选择，选择UCB最大的那个action。

MCTS玩tic-tac-toe

下面分别在人走先手和agent走先手的情况下，演示了我实现的MCTS：

人走先手

最后打成了平局。

MCTS Agent走先手

MCTS Agent赢了（人放了点水）

问题

迭代次数的影响

本以为对于tic-tac-toe这样简单的游戏，迭代次数不需要特别大，然而似乎并不是这样，当迭代次数分别为1000，5000，10000时，MCTS给出的最佳走法有概率不一致。

（我检查了好几遍我的代码，没找到问题所在，不知道是我的实现问题，还是MCTS的缺陷）

比如，当Human走先手，下了这一步棋之后：

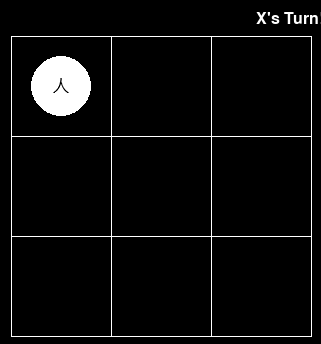
现在MCTS需要计算这个state下，最优的下法，当MCTS的迭代次数为1000时，重复100次MCTS算法，MCTS有 77次选择中间这一步，23次选择其他位置。

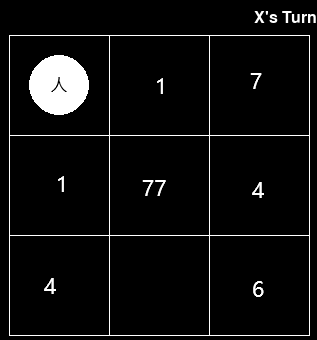
当迭代次数为 5000 的时候， MCTS有97次选择中间这一步，3次选择其他位置。

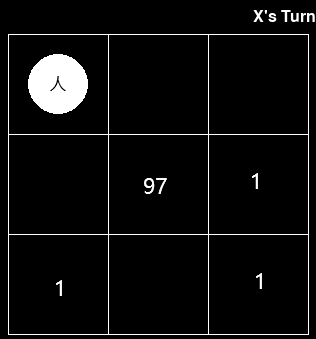
当迭代次数为 10000 的时候， MCTS有99次选择中间这一步，1次选择其他位置。