[算法] 平方根倒数速算法中的魔数0x5f3759df的来源

引子

平方根倒数速算法 即 Fast Inverse Square Root算法 [3]，是一个相当出名的算法，其具体作者已不可考，由于雷神之锤中大量使用了该种算法使得它为人所知。

为什么需要平方根倒数而不是平方根本身？因为图形学中大量运算需要用到平方根倒数，而不需要平方根，比如 向量的normalize()操作 $\frac{1}{\sqrt{x^2 + y^2 + z^2}}(x,y,z)$ 就包含平方根倒数；而图形学中每一帧的渲染都至少需要调用上万次normalize。如果能加速平方根倒数的计算，那么渲染的速度将会大大提升。

该算法诞生于20多年前，如今，该算法仅具有研究价值，但不具备使用价值[1]，CPU已经内置了速度更快，误差更小的指令；我们只需要使用 1/sqrt(y)。

不过，这不影响我们去理解这个算法的精妙之处，在短短4行C代码里面，涉及了 1) IEEE 754标准 2) C 语言的undefined behavior 3) 牛顿迭代法。

这里的重点是第二步，即如何推导出magic number 0x5f3759df，更细节的部分可以参考 [2] [4]。

算法

//from wikipedia [3]
float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;
	x2 = number * 0.5F;
	y  = number;
    
    /*核心代码*/
    // 1. reinterpret_cast from float to int
	i  = * ( long * ) &y;                       // evil floating point bit level hacking（对浮点数的邪恶位元hack）
    // 2. 估算平方根倒数
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
    // reinterpret_cast from int to float
	y  = * ( float * ) &i;
  	// 3. 牛顿法
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration （
//      y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

	return y;
}

算法大致分为3部分：

• reinterpret_cast 用于在float和int之间相互转换，否则任何一个编译器都会禁止对float型做位运算。
• 利用magic number 0x5f3759df估算平方根导数（见下文）
• 一次牛顿迭代法（见下文）

估算平方根导数

IEEE 754标准中，32位浮点数包含1个符号位，8位指数 $E$，23位尾数 $M$，任一浮点数可以被表示为：$(1.M) \times 2^{E - 127} = (1 + \frac{M}{2^{23}}) \times 2^{E - 127}, M \in[0, 2^{23} ), E \in [0,256)$ .

目标：需要计算 $y$ 的平方根倒数 $\frac{1}{\sqrt{y}} = y^{-\frac{1}{2}}$， $y$ 的 IEEE 754形式为 $y = (1 + \frac{M_y}{2^{23}}) * 2^{E_y - 127}$.

出于数学上的直觉，我们将 $y$ 取以2为底的对数：

$$\begin{align} \log y &= \log{((1 + M_y) * 2^{E_y - 127})} \\ &= \log{(1+\frac{M_y}{2^{23}})} + E_y - 127 \end{align}$$

$\frac{M_y}{2^{23}}$ 显然是在 $[0,1]$ 这个区间上，而在这个区间中，有$\log(1+x) \approx x$；

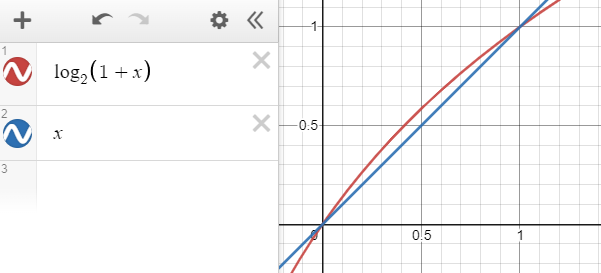
如果再加上某个常数 $\mu$，那么这个给近似效果会更好一些：

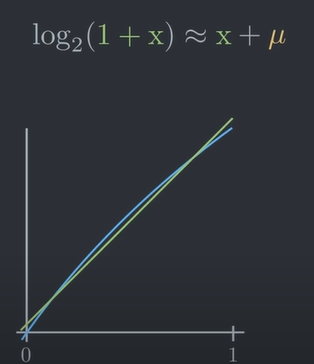
使用这个近似，可以进一步简化：

$$\begin{align} \log y &= \log{(1+\frac{M_y}{2^{23}})} + E_y - 127 \\ &\approx \frac{M_y}{2^{23}} + \mu + E_y - 127 \\ &= \frac{1}{2^{23}}(M_y + E_y * 2^{23}) + \mu - 127 \end{align}$$

而 $M_y + E_y * 2^{23}$ 正是 float型 y 被转型为 int 型后的值。

现在对 $y^{-\frac{1}{2}}$ 同样取对数：

$$\log y^{-\frac{1}{2}} = -\frac{1}{2} \log y \approx -\frac{1}{2}\left( \frac{1}{2^{23}}(M_y + E_y * 2^{23}) + \mu - 127 \right)$$

假设 $y^{-\frac{1}{2}}$ 的准确值为 $A$，其指数和尾数部分分别为 $E_A$ 和 $M_A$，同样对 $A$ 取对数：

$$\log A \approx \frac{1}{2^{23}}(M_A + E_A * 2^{23}) + \mu - 127$$

则以上两式用不同的方式表达了 $\log A $ 即 $\log y^{-\frac{1}{2}}$ ，故联立以上两式可解得 $M_A + E_A * 2^{23}$：

$$\begin{align} \log A &= \log y^{-\frac{1}{2}}\\ -\frac{1}{2}\left( \frac{1}{2^{23}}(M_y + E_y * 2^{23}) + \mu - 127 \right) &= \frac{1}{2^{23}}(M_A + E_A * 2^{23}) + \mu - 127 \\ \end{align}$$

略去中间过程，可得：

$$\begin{align} M_A + E_A * 2^{23} &= 2^{23} * \frac{3}{2}(127 - \mu) - \frac{1}{2}(M_y + E_y * 2^{23}) \\ \end{align}$$

第一项中的 $\mu$ 取 $ 0.0450461875791687011756$ 时[3]，第一项的结果为 $1597463011$，16进制表示为 0x5F3759e3；如果将第二项的 $\frac{1}{2}$ 变为移位运算，则上式和代码中的 这一行无比相近

i  = 0x5f3759df - ( i >> 1 );  

只是magic number差了一点点，如果 $\mu$ 的值恰当，应该可以得到完全一样的数字。

牛顿迭代法

牛顿迭代法的更新公式为：

$$x_{t+1} = x_t - f(x_t) / f^\prime(x_t)$$

牛顿迭代法的前提条件：要求初始点在函数零点附近，因为i = 0x5f3759df - ( i >> 1 );所估算的结果误差应该不大，可以认为前提条件已经满足。

此时，我们的问题为，已知 $y$， 需要求 $x$ 使得 $\frac{1}{\sqrt{y}} = x$，即 $\frac{1}{x^2} = y$，移项得$f(x) = \frac{1}{x^2} - y = 0$ ，对 $f(x)$ 应用牛顿迭代可得迭代公式为：

$$\begin{align} x_{t+1} &= x_t - f(x_t) / f^\prime(x_t) \\ x_{t+1} &= \frac{3}{2}x_t - \frac{y}{2}x_t^3 \end{align}$$

翻译成代码就是：

y  = y * ( threehalfs - ( x2 * y * y ) );

参考资料

[1] Is fast inverse square root still used? https://www.quora.com/Is-fast-inverse-square-root-still-used

[2] Fast Inverse Square Root — A Quake III Algorithm https://www.youtube.com/watch?v=p8u_k2LIZyo

[3] wiki-平方根倒数速算法 https://zh.wikipedia.org/zh-hans/%E5%B9%B3%E6%96%B9%E6%A0%B9%E5%80%92%E6%95%B0%E9%80%9F%E7%AE%97%E6%B3%95

[4] 论文 https://www.lomont.org/papers/2003/InvSqrt.pdf