[Paper][RL][Nature 2018] AlphaGo Zero: 无需监督学习的AlphaGo

论文地址：不可下载，可下载，草稿

辨析：AlphaGo有好几个版本，按照时间顺序：AlphaGo Fan（即AlphaGo paper），AlphaGo Lee，AlphaGo Master，AlphaGo Zero（下文中有时会称之为Zero, this paper），AlphaZero（后续工作，Science Paper）。他们之间的区别参见 这篇论文的附录。

引子 & 总结

AlphaGo 确实超越了顶尖人类棋手（AlphaGo Lee 4:1打败了李世石），但是，AlphaGo无论是在成绩上还是算法上，还有很大的提升空间。

• 从成绩角度来谈，成熟的围棋AI需要对人类有绝对100%的胜率，而不是负于李世石一盘。

• 至于AlphaGo的算法，从我的角度来看，最不自然的一点，就是train test的流程 不一致。按照深度监督学习的观点，如果想模型在测试集上的表现尽可能接近训练集上的表现，需要保证测试的流程和训练一致，否则会严重损害模型性能。然而，在AlphaGo的训练阶段，没有MCTS的参与。

  此外，现在深度学习追求的是end2end，而AlphaGo的training pipeline显得不够elegant。

• 最后是这篇文章所强调的核心，Mastering without Human Knowledge。用DL的话讲，就是不需要监督学习预训练和围棋专家数据集，只用强化学习的技术。

于是 AlphaGo Zero的算法相比于AlphaGo有了以下提升：

1. 保证了train test 的一致性，都包含了APV-MCTS
2. 抛弃了pipeline，用一个网络代替了所有网络
3. 移除了MCTS中的rollout阶段，完全由 value network决定。
4. 用 MCTS 提升 policy network 输出的action probability，并作为 label，训练policy network。

算法

Zero 的 训练方式可以看作是 off-policy的，一边在与环境交互（self-play）并把样本存入一个replay memory中；一边在做神经网络的训梯度下降（optimization)。

所以，算法由2部分构成：self-play, optimize(sgd)。还有一个相对不太重要的部分为 Evaluation。三个部分之间是并行执行的。

1. Self-play with MCTS

Self-play的目的是在为 optimize阶段生成训练数据。

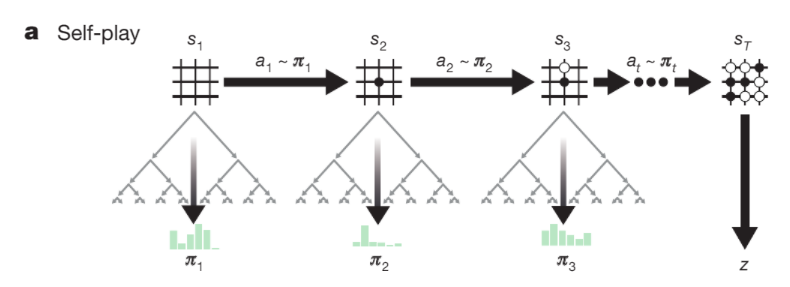
和AlphaGo APV-MCTS的区别： 如果我对附录中的search algorithm理解没错的话，这部分和AlphaGo基本没有区别，除了省略了rollout（下式中 $\lambda = 0$ ，只根据value network 的输出来确定叶子结点的value）以及expand的方式。

$$V\left(s_{L}\right)=(1-\lambda) v_{\theta}\left(s_{L}\right)+\lambda z_{L}$$

具体的Self-play流程：

• 在每个state $s_t$ 处 执行MCTS，MCTS的每次simulation重复以下步骤：

1. selection: （与AlphaGo中完全一样），用下式选出best edge/action：

   $$a_{}=\underset{a}{\operatorname{argmax}}\left(Q\left(s_{t}, a\right)+u\left(s_{t}, a\right)\right)$$

2. expand: （与AlphaGo中不同，总是expand）重复selection直到叶子节点，扩张。利用 current best network计算出 $P(s,a)$ 作为edge 的先验概率。

3. rollout: 无。

4. backup: （与AlphaGo中完全一样）利用 current best network计算出 叶子节点的 value $V(s^{\prime})$，对从root到叶子节点上的这条path上的所有结点更新 $Q, N$。

• MCTS结束之后，在root处，获取每个edge的 $N(root,a)$，并计算该action 的 概率 $\pi_a$:

$$\pi_{a} \propto N(s, a)^{1 / \tau}$$

所有action 的概率组成了一个向量 $\pi_t$ ，则当前这个state的transition为 ：$(s_t, \pi_t , z_t)$。其中 $z_t$ 的值只有当这一盘围棋结束后才得知。

• 当前state的动作 $a_t$ 采样于 $\pi_t$，和 (stocastic) Policy Gradient 中action 的获取方式一致：

$$a_{1} \sim \pi_{1}$$

• 当这一盘围棋结束之后（黑或白胜），得到 reward $z = \pm1$，则这一盘围棋的所有transition 的 $z_t = z$，并将所有transition $(s_t, \pi_t , z_t), t = 0,1,2,….$ 全放入Replay memory中。Memory 大小为 500,000，淘汰最旧的。

2. Optimize with replay memory

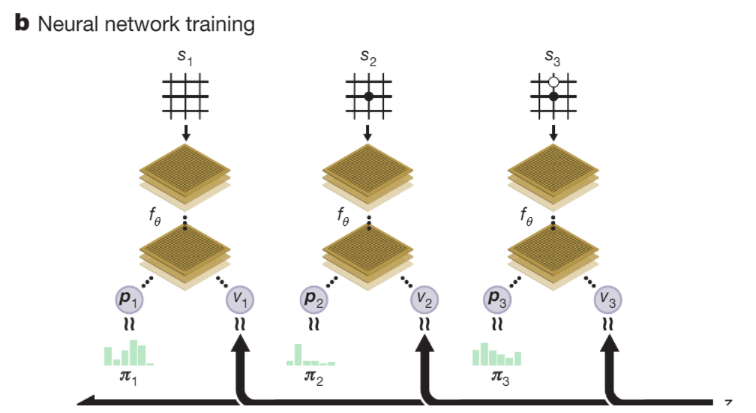
这部分比较简单：

1. sample uniformly from replay memory.

2. X = $s_t$ 。对于 policy 分支，Y = $\pi_t$ , 损失函数为cross entropy，对于 value 分支，$Y = z_t$ ，损失函数为 平方误差函数，再加上 L2 norm：

   $$l=(z-v)^{2}-\boldsymbol{\pi}^{\mathrm{T}} \log \boldsymbol{p}+c\|\theta\|^{2}$$

   注：一般如果有两个branch，它们之间的loss会由一个超参进行调节，比如：

   $$l=\lambda(z-v)^{2}-\boldsymbol{\pi}^{\mathrm{T}} \log \boldsymbol{p}+c\|\theta\|^{2}$$

   在这篇论文附录里提到了，$\lambda = 1$ 即 两个loss权重一样。

3. 利用mini-bach SGD训练网络。

3. Evaluation

每1000次 mini-BSGD之后，会存一个checkpoint a 。由于网络训练有波动，需要确保用最好的网络self-play生成训练数据。于是，作者让 a 和 current best network进行400局对弈，如果a胜出55%，则current best network = a。

同时，Evalutaion可以一直跟踪checkpoint的表现，保证网络不会diverge。

不过，在后续工作AlphaZero中，作者移除了400局对弈这一步，直接current best network = a。

网络结构

从AlphaGo中的4个网络，简化成了1个网络，输入为棋局（以及过去几步的棋局，类似于DQN的输入有4帧），共享feature extractor，末端有两个分支，分别为policy branch：输出#actions 的概率；value branch： 棋局的value $V$ 。

相比于AlphaGo中的网络，这篇论文的网络要深一些，并且与时俱进，引入了BN和残差网络。实验部分为了消除网络带来的影响，做了相关的实验，有兴趣的可以看看，这里省略了。

输入相比于AlphaGo减少了一些，为19x19x17。17 = 8（8 most recent position，类似DQN的输入为4帧) + 8（8 most recent position of opponents）+ 1 （which player）

Experiments

1. Evaluation VS AlphaGo

首先，最重要的就是AlphaGo Zero的效果，在围棋里面就是Elo rating。

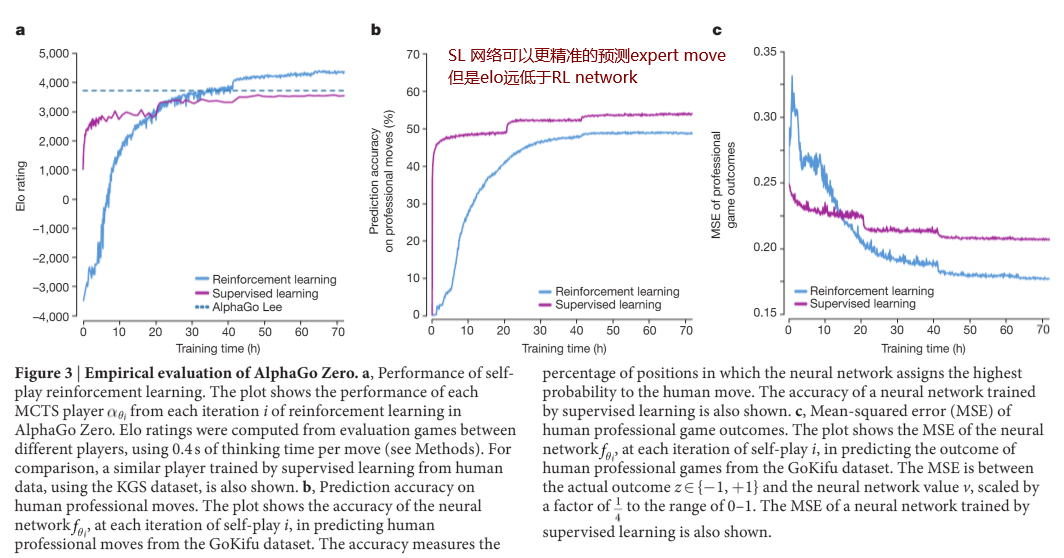
1. 图中可以看出AlphaGo Zero的Elo大幅超过了 AlphaGo Lee，这可以说明，AlphaGo Zero确实是比AlphaGo 更好的算法。此外，它们对战时，AlphaGo Zero以100：0的绝对优势胜出。
2. 尽管人类棋手数据训练出的 SL network在预测expert move 上更准确，但是Zero 却拥有更高的胜率。这意味着Zero找到了比人类棋手更优的解法。
3. Elo 4000+已经远超人类棋手了，目前世界第一的Elo才为 3600分。

2. 不同时期学到的不同Knowledge

Zero训练的总时间为72h，作者展示了在不同训练阶段中Zero进行自我对弈self-play时，所生成的棋局。由于图比较大，这里就不放了。

总的来说，在训练早期，Zero 的策略主要是贪心的，想要尽快围住对面，吃掉对面的棋子；在训练中期，Zero的眼光开始放的比较远，不再纠结于一棋一子的得失。在训练后期，Zero的大局观逐渐形成，打法多变，远超普通人类所能达到的水平。

3. Final Performance

作者最后训练了一个终极版AlphaGo Zero，从29 million盘棋中学习了40天，结果如下：

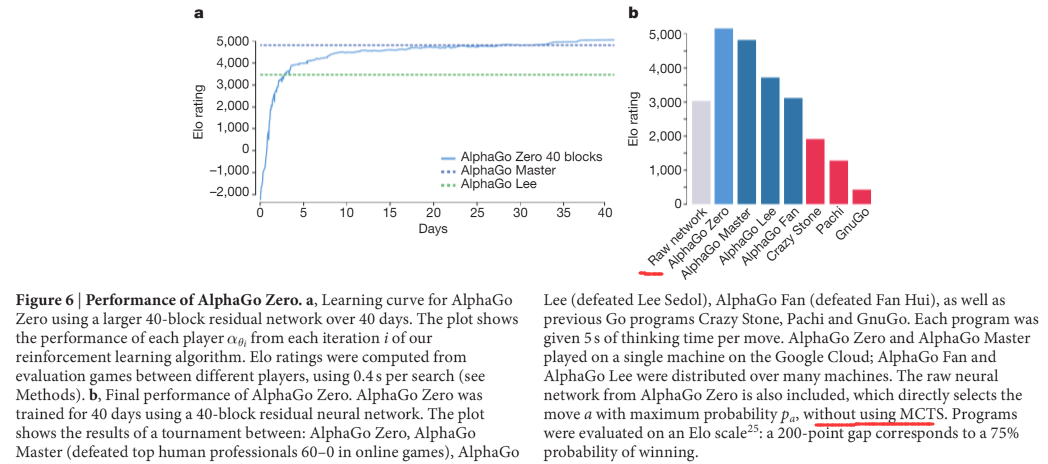
有几点值得注意的：

1. 纯端到端 DL 的方法 （raw network）与 DL + MCTS 的方法差距甚远。个人认为，这是因为围棋的可能的position数目过于庞大，不足以生成足够大量的样本让网络充分学习。然而，如果引入MCTS方法，那对于神经网络的要求不需要太高；在MCTS中，会从root向树的深处探索，而处于树深处的state，无论是policy还是value ，相比于root处，网络都会预测的都更精确一些，这使得最终MCTS给出的的 $\pi_t$ 显著优于只使用policy network得出的 action probability。所以，作者称MCTS为 policy improvement operator。
2. ELO 达到 5000，训练时间40天。。除了Google估计其他企业以后也不太会继续在围棋上做研究了，除非硬件或深度学习理论层面有革新。

参考资料

[1] AlphaGo

[2] Policy Gradient Therom, NIPS 1999