[Paper][RL][Nature 2016] AlphaGo: Deep RL 与 Tree Search 的成功结合

强化学习 MCTS Model-Based RL
强化学习
发布日期:   2021-08-10
更新日期:   2022-06-01
文章字数:   3.4k
阅读时长:   13 分

论文：Mastering the game of Go with deep neural networks and tree search, AlphaGo

总结

AlphaGo 结合了 Deep RL, Deep SL 与 Tree Search 。AlphaGo 的 训练方式并不是end2end的，但是取得了非常优秀的结果，将围棋算法的水平从 业余 直接提升到了职业5段。

AlphaGo 的 贡献可以总结为2个部分：

  • APV(Asynchronous policy and value)-MCTS：AlphaGo 算法的雏形来自于MCTS算法，蒙特卡洛树搜索。然而直接将MCTS应用在围棋上是非常困难的，为此，作者设计了几个网络来魔改MCTS，称之为 APV-MCTS：
  1. rollout policy nework: vanilla MCTS 的 rollout policy 是 完全随机的，在围棋这种巨大搜索空间下，完全随机的policy 得到的 estimated value显然是非常不准确的（见算法 4 Value network小节的图）；但是太过复杂的rollout policy又会增加时间成本，减少rollout的次数。综合以上两点，rollout policy的网络结构为线性网络。
  2. SL policy network: 在MCTS扩张的过程中，不能盲目的扩张，应该向着比较promising的方向扩张，这样才可以尽可能深的探索。为此，作者设计了SL policy network，给出了MCTS每条边的先验概率。
  3. value network: 局势评估函数。由于搜索空间过大，有限时间内，仅凭rollout不能得出准确的value。为此，作者设计了 value network。综合 value network的预测和rollout的结果，才得到最终的value用于backup。

APV-MCTS仍然是在MCTS的框架下，分为4步，selection，expand，rollout，backup。

  • AlphaGo Pipeline: 作者结合了监督学习和强化学习，分为多个步骤训练value network。

引子

不考虑强化学习，想想看如何利用监督学习实现围棋算法 [2]：

直接给围棋 AI 看人类围棋大师的棋谱，让它预测人类大师的下棋位置。很显然，这就是一个分类问题：输入当前棋局状态，输出落子位置。2015年之前最强的基于监督学习的围棋 AI 也只能达到 35% 的分类准确率，根本没法跟人类顶尖棋手过招。

强化学习应用在围棋上的问题：

  • 状态太多，search space太大，但不是major concern，在 9x9的小围棋盘上就很难了。

image-20210721004835680

  • 没有一个好的评估局势的方法。象棋则很好评估局势，棋子比对方多则分数高，强力棋子的权重更大，Artificial Intelligence A Modern Approach中minmax那一章详细介绍了国际象棋的评估函数。但是，围棋，很难用一个简单的方法判断局势的好坏。

    image-20210721005533762

MCTS的引入大幅提升了围棋的强化学习成绩。因为MCTS不需要局势评估函数，MCTS会用rollout policy（或叫default policy）一直走到棋局结束，并不会在中途终止。当然由于rollout policy是随机的，围棋的搜索空间又很大，可以想象MCTS的效果也是相当有限的，在AlphaGo之前，MCTS方法在Go上的最好水平相当于weak amateur player[1]。

算法 APV-MCTS

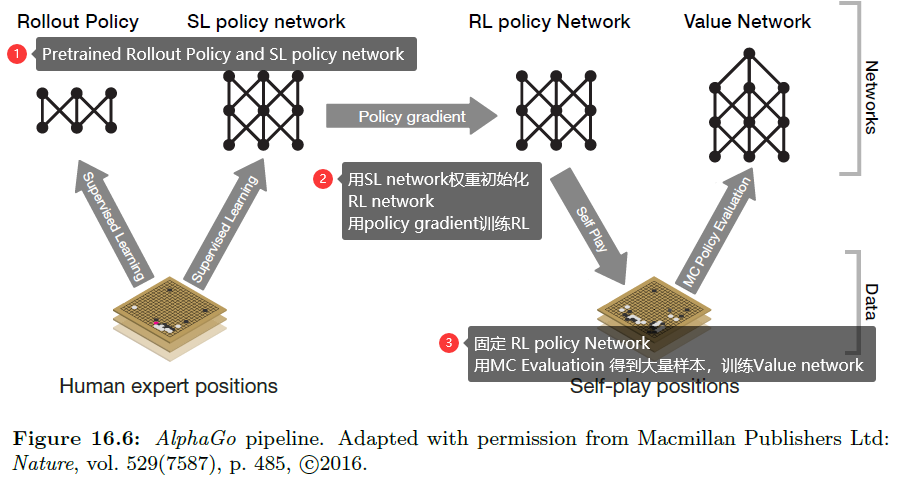
AlphaGo Pipeline

0. 为什么使用CNN

SL, RL, Value Network 的结构几乎相同，都是以 CNN 为骨架。在Atari这种视频游戏上使用 CNN是很自然的，那么围棋使用CNN的理由在哪里呢？AlphaGo这篇论文中没有解释，AlphaZero[4]中提到了，是因为围棋的规则和CNN的特点匹配：

AlphaGo Zero (and AlphaGo) used a convolutional neural network architecture that is particularly well-suited to Go: the rules of the game are translationally invariant (matching the weight sharing structure of convolutional networks) and are defined in terms of liberties corresponding to the adjacencies between points on the board (matching the local structure of convolutional net-works).

1. SL policy network

（目的在于模拟人类棋手）

SL 意为 Supervised Learning，所以是 SL Policy Network $p_{\sigma}(a \mid s)$ 的训练完全是监督学习的分类问题。

网络结构：13 conv，输出层为softmax，#class =19x19，代表棋盘上每一个落子点。

既然是监督学习：

  • X = state, 维度 为 19 x 19 x 48，即每个落子处用48维特征表示（48维每一维的作用见论文附录表20）
  • Y = action，19x19维 one-hot vector。
  • SL network在测试集上的分类准确率是 57.0%。考虑到这是个 19x19 分类问题；且 state space太大，很可能遇见训练时未见过的情况，这个准确率相当不错了。

值得注意的是，每个落子处有48个features，尽管这仅仅对SL Policy network 的分类准确率只有1.3% 的提升，但是 这 1.3%的提升可以使得最终的AlphaGo的win rate有比较大的提升。（见下图）

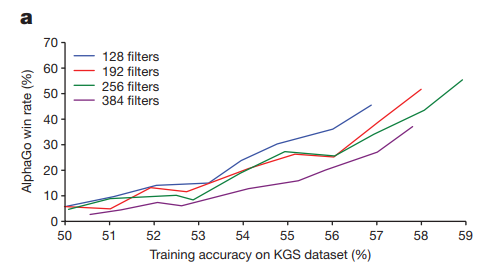
image-20210810205414938

2. rollout policy

rollout policy $p_{\pi}(a \mid s)$ 为 SL network丐版，训练方式一样，只是网络只有一层，是个线性模型，准确率仅有 24.2，但是做一次分类只需要 2us，而 SL network需要 3ms。

3. RL policy network

RL policy network $p_{\rho}(a \mid s)$ 是用RL的方法（policy gradient）训练 监督学习预训练过的模型（SL policy network）。

SL policy network是通过学习人类棋谱训练的。然而，毕竟人的算力有限，人类棋谱在绝大部分情况下都是sub optimal的，这样学习得到的SL network的成绩有限。

于是，作者引入了policy gradient 方法，来训练 RL network（ 用训练好的SL network 的权重初始化），$z_t$ 就是 $G_t$ ：

（根据上式来看，这里似乎使用的vanilia Policy gradient ，即 论文 Policy Gradient Therom 中提出的方法，而不是Actor Critic，原因可能是Actor Critic需要一个value network作为critic，这对于RL policy network是一个鸡生蛋蛋生鸡的问题）

SL network只能说是在”模仿人类下棋“，但是RL network在 “为了赢而下棋”。论文中将SL network 和 RL network进行了对战，RL network 胜率为 80%。

4. Value network

Value network $v_{\theta}(s)$ 是一个局势评估函数，目的是判断当前局面的好坏。

在这篇论文里，Value network的训练仍然是一个监督学习的回归问题，先固定住RL policy network进行self-play收集大量数据，然后利用这些数据进行Value network 的监督学习。所以，$v_{\theta}(s)$ 是 RL policy 的 evaluation：

  • X: state
  • Y: $G_t = \pm1$
  • 样本生成方式：2 个 RL policy network 相互对战形成episode，每个episode可以生成许多个 $(X,Y)$ pair。 将这些 $(X,Y)$ shuffle 得到数据集。
  • 网络结构：和SL/RL network相同，只是输出从 19x19 变为了 1。

我个人看论文中的一些问题：

  1. DQN不也是学习一个value network吗，为什么DQN是强化学习算法，需要一边训练一边收集transition；而这里是一个监督学习问题？

答：因为DQN中所evaluate的policy是时刻在变化的，而这里仅仅是在evalute RL policy network。所以是监督学习问题。

  1. 另一个问题是，为什么学习 $v $ 而不是 $Q$？

答：没有必要，可以参看 [3] 中 Afterstate那一节。

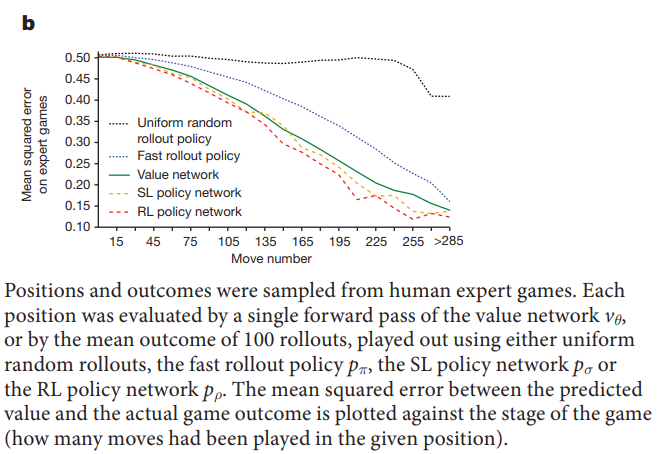
value network的准确性： 作者对比了 value network(不需要rollout) 和 各种policy经过100次rollout 估计出的 value 与 groudtruth之间的MSE，可以看到，value network的MSE与 RL policy相差无几。然而，RL policy 做 100 次 rollout需要的时间是 value network跑一趟的15000倍。

image-20210810205710365

5. APV-MCTS

综合上述网络，可以得到APV-MCTS。在APV-MCTS中，每条边持有：$N(s,a)$ 访问次数， $u(s,a)$ SL network计算的 prior probability，$Q(s,a)$ 平均获胜概率，又叫expected return。

  1. Selection: 根据以下式子从 root 开始进行selection，直到叶子节点。

    当该节点初次加入树时，prior probability $P(s,a)$ 由 SL network计算得到，为选取每个动作的概率。每个动作（即每条边）的 $P(s,a)$ 只计算一次，此后不再变化。 $u$ 的作用是，随着访问次数 $N$ 的增加，逐渐鼓励exploration。

    当到达某个叶子结点 时，selection停止。如果该叶子结点不是terminal state，进行expand。

    注：这里不太严谨，在 这篇论文里，叶子结点并不是总是expand，需要满足一个条件（见附录）。但是在后续工作AlphaGo Zero中，叶子节点总是expand。

  2. Expand: 如上所述，新结点$s_L$ 的每条边会存入 SL network 计算的$P(s,a)$，并初始化 $N, Q$。

  3. Simulation:

    从新结点出发，重复使用 rollout policy 一直到terminal state，得到reward $z_L$ 。再用value network估计 $s_L$ 的 value。两者综合得出 从 $z_L$ 出发，获胜的平均概率 $V(s_L)$：

  4. Backup: 对于自 root 到 $s_L$ 上的所有edge，更新其上的 $Q, N$ ：

    论文中的公式比这个复杂，但是意思是一样的。

    和vanilla MCTS一样，要注意 $V$ 的正负号，每往上一层，都要 反号。

  5. 决策阶段，即当MCTS树生成完成之后，会在root选择访问次数最多的一条边，$argmax_aN(root,a)$。

有几点需要注意的：

  • 先验概率 $P$ 非常重要，它一定程度决定了 每条边的访问次数，因为一开始所有边的 $Q = 0$，selection规则 $a_{t}=\underset{a}{\operatorname{argmax}}\left(Q\left(s_{t}, a\right)+u\left(s_{t}, a\right)\right)$ 相当于是在选择先验概率最大的 边。
  • 虽然在前面提到了，RL network 比 SL network 的 win rate 更高，但是先验概率 $P(s,a)$ 是由 SL network而不是 RL network计算得到的，这一点比较值得考究。但是，作者通过实验发现，与人类对战时，使用 SL network计算 $P(s,a)$ 的效果强于 RL network。作者推测这是因为 SL network的行为更接近人类棋手（人类棋手会从很多种落子的可能种选择比较优的一个），而 RL network更倾向于 寻找最优解，落子的位置很单一；这使得在于人类对战时，使用更接近人类行为模式的 SL network 的效果更好。

Experiments

时间复杂度

MCTS的特点之一是在live play 时实时演算，这使得复杂度不高的vanilla MCTS的耗时就很长了，引入了 DL 的 APV-MCTS 每一步的耗时就更是多出了几个数量级。

不过，Google本来就是分布式计算的引领者，GFS、MapReduce都是出自Google，实现一个分布式的AlphaGo 不是难事。论文实现了2个版本：

  • 多线程版本：40 APV-MCTS search threads, 48 CPUs(MCTS simulation), 8GPUs(value network/ SL policy network).
  • 分布式版本：40 APV-MCTS search threads, 1202 CPUs(MCTS simulation), 176GPUs(value network/ SL policy network).

两个版本每一步MCTS的时间都是 5s，但是分布式版本在相同的时间里可以进行更多次的simulation，决策更好，win rate 更高。

AlphaGo Evaluation

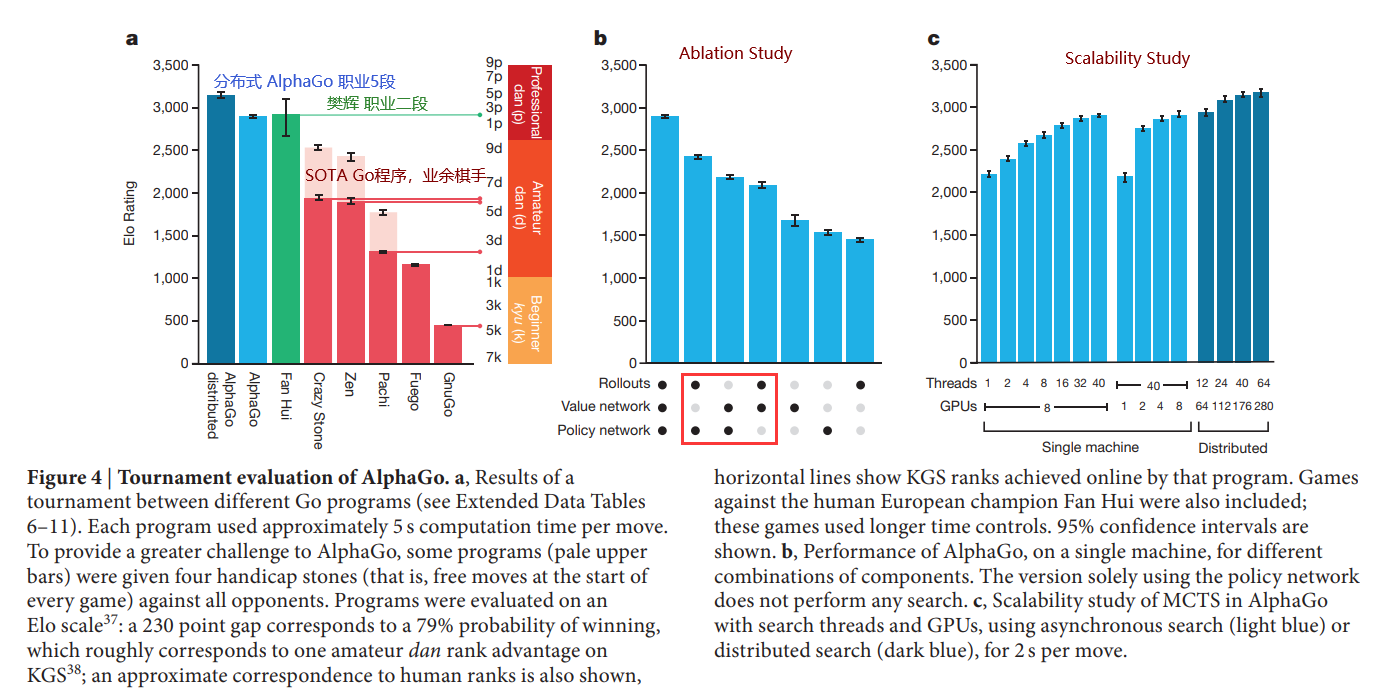
image-20210811170205762

这张图信息量很大，先从图a开始说起：

  1. 樊麾（1981年12月27日－），中国大陆出生的法国职业二段围棋棋士。

    2015年10月，樊麾受邀与Google DeepMind所研发出的AlphaGo进行分先五局竞赛，AlphaGo以5:0全胜的纪录击败樊麾[4]；樊麾成为世界上第一个于十九路棋盘上，以分先手合)被围棋软件击败的职业棋手。

    —— wiki

    他也算在人类历史上留下了自己的印记，比许多八九段的还要出名。

  2. MCTS是一种耗时可长可短的算法，耗时只与simulation次数有关，论文里统一规定了耗时为5s（或2s）。

  3. Elo Rating 听上去像是 某种 在线游戏的天梯分，但其实是适用于各种对弈、对战的等级划分系统。

图b是Ablation Study：

  1. 第二列为不使用 value network，即 $\lambda = 1$ ，此时elo下降明显，这说明 对于围棋这种 搜索空间极大的env，只使用rollout完全不足以在有限时间中得出比较准确的 $V(s_L)$ ，需要 value network 的辅助。

    第三列为不使用 rollout，此时elo下降更为明显，这说 value network预测的 $V(s_L)$ 也不够准确。只有rollout 与 value network结合才能得出比较准确的 $V(s_L)$ 。

    value network本质上是 $p_\rho$ 的policy evaluation，所以value network的输出的意义是从 $s_L$ 不断执行 $p_\rho$ 的expected return；而rollout 是 在估计 rollout policy $p_\pi$ 的 expected return，作者认为两者是互补的。

  2. 令我意外的是，不使用policy network时，elo下降最为明显。论文中没有提原因，但我觉得，SL policy network的作用是指导MCTS的探索方向，使APV-MCTS在promising方向在有限时间内探索比较深的距离；而不用把有限的时间浪费在一些完全错误的分支上。

  3. 后三列不做解释了，论文中也没有提。

图c略。

可视化

论文中图5展示了APV-MCTS的可视化结果：

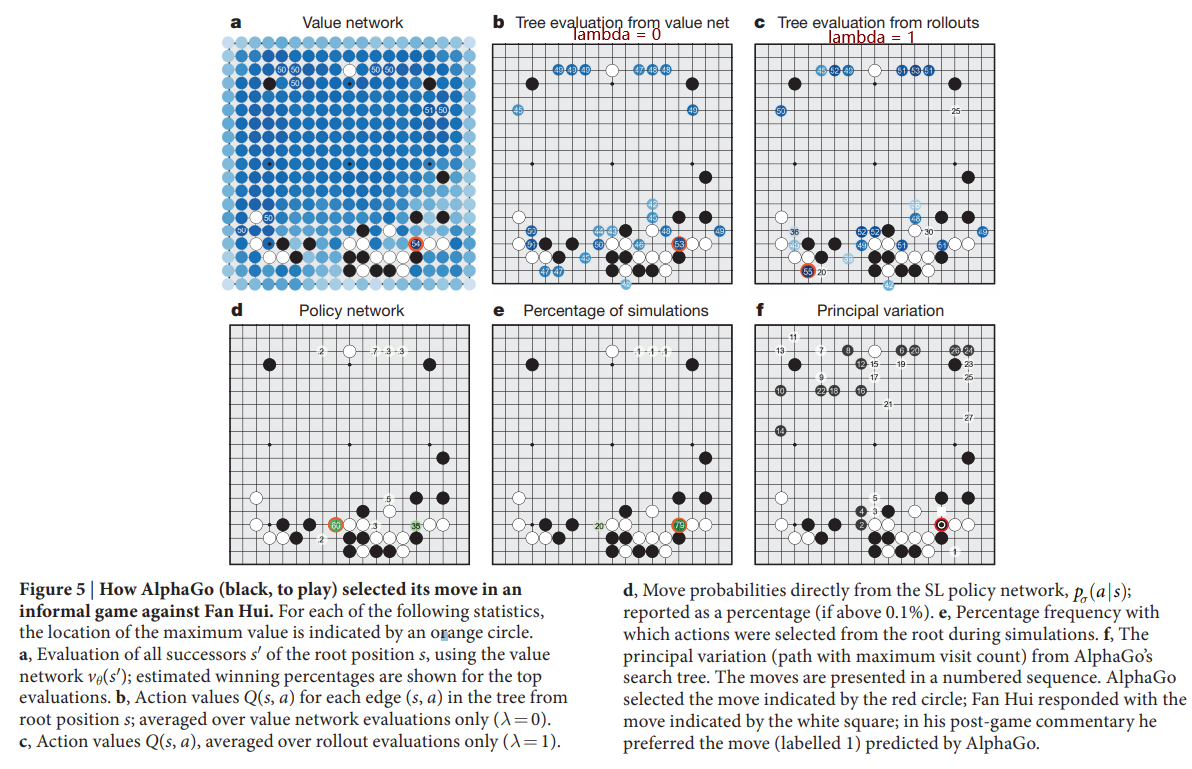
image-20210811174507745

图 a,b,c,d,e都是self-explained的，这里说一下 f：

  • Principal variation是指从MCTS root出发，每次选择most visited edge，直到MCTS叶子节点为止的这条路径。可以理解为MCTS所得出的最佳走法。
  • AlphaGo下了这一步（红色）之后，它认为对手下 label = 1这一步是最优的。然而，樊麾下了另外一步。复盘时，樊麾认为AlphaGo的走法是更好的。

参考资料

[1] AlphaGo

[2] https://mp.weixin.qq.com/s?__biz=MzA5MDE2MjQ0OQ==&mid=2652786766&idx=1&sn=bf6f3189e4a16b9f71f985392c9dc70b&chksm=8be52430bc92ad2644838a9728d808d000286fb9ca7ced056392f1210300286f63bd991bde84#rd

[3] RL, an introduction 2nd, Sutton et al

[4] AlphaZero Science 2018

文章作者: GeT Left
文章链接: http://example.com/2021/08/10/ml/qiang-hua-xue-xi/paper/alphago/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 GeT Left !
强化学习 MCTS Model-Based RL
  目录