[Paper][RL][ICML 2017] Distributional RL

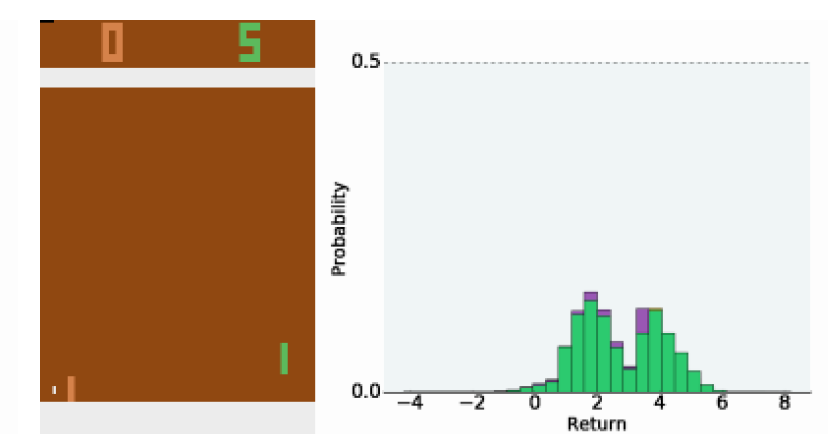
论文：ICML 2017 A Distributional Perspective on Reinforcement Learning

引子 & Motivation

Motivation & idea: Approximate value distribution instead of expected return.

然而，idea虽然简单，实现起来却并不容易。最简单的想法使用一个 高斯分布 对 $Q$ 建模，然而这其实与 approximate expected return区别不大。这篇文章采取的是另一种方法，这使得所拟合的分布不仅限于 单峰形态的概率分布函数（比如 高斯分布）：

理论

略

算法

1. 区间离散化

如何方便的建模任意的概率分布函数呢？作者使用了一个离散分布来建模：

1. 将 $[V_{min}, V_{max}]$ 上均匀采样 $N$ 个点，$z_0, z_1, …z_{N}$。（$V_{min}, V_{max}, N$ 是三个超参，在本文的实验部分，使用的超参为 $-10, 10, 51$，即相邻点的相差 $0.4$。

2. 每个点的概率 为

   $$P[Q(x,a) = z_i] = p_{i}(x, a)=\frac{e^{\theta_{i}(x, a)}}{\sum_{j} e^{\theta_{j}(x, a)}} (0 \le i < N)$$

   这里的 $\theta_{i}(x, a)$ 为需要学习的神经网络，神经网络的输出通过归一化转化为概率。

2. Projected Bellman Update

DQN中的target value 为 ：

$$Q_{target}(s_t,a) = R + \gamma Q(s^{t+1}, a^*)$$

这篇论文中的target distribution为：

1. 计算 next state 的 best action $a^*$ 的distribution：

   $$\begin{aligned} &Q\left(x_{t+1}, a\right):=\sum_{i} z_{i} p_{i}\left(x_{t+1}, a\right) \\ &a^{*} \leftarrow \arg \max _{a} Q\left(x_{t+1}, a\right) \end{aligned}$$

2. 计算 离散点 $z_j$ 经过Bellman Update后所处的位置：

$$\begin{aligned} &\hat{\mathcal{T}} z_{j} \leftarrow\left[r_{t}+\gamma_{t} z_{j}\right]_{V_{\mathrm{MIN}}}^{V_{\mathrm{MAX}}} \end{aligned}$$

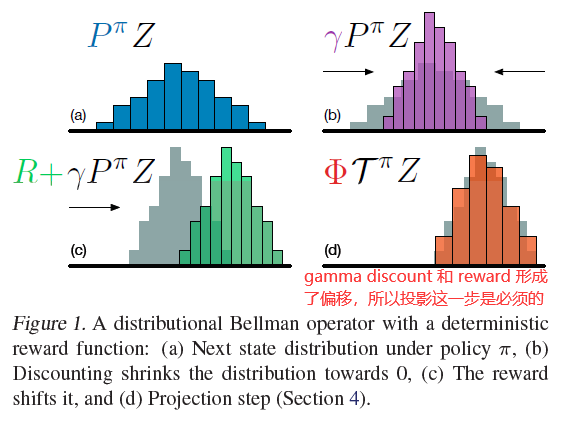
1. 由于 $\gamma$ 和 $r_t$ 影响，Bellman Update之后的 $\hat{\mathcal{T}} z_{j}$ 可能并不在预先设好的离散点 $z_0, z_1, …z_{N}$ 上。于是根据 $\hat{\mathcal{T}} z_{j}$ 与相邻离散点 $l,u$ 的 距离将 $p_{j}\left(x_{t+1}, a^{*}\right)$ 分配到 $l,u$ 上。（ $l,u$ 是 $z_0, z_1, …z_{N}$ 中的点）：

$$\begin{aligned} &b_{j} \leftarrow\left(\hat{\mathcal{T}} z_{j}-V_{\mathrm{MIN}}\right) / \Delta z \quad \# b_{j} \in[0, N-1]\\ &l \leftarrow\left\lfloor b_{j}\right\rfloor, u \leftarrow\left\lceil b_{j}\right\rceil \text { # Distribute probability of } \hat{\mathcal{T}} z_{j}\\ &m_{l} \leftarrow m_{l}+p_{j}\left(x_{t+1}, a^{*}\right)\left(u-b_{j}\right)\\ &m_{u} \leftarrow m_{u}+p_{j}\left(x_{t+1}, a^{*}\right)\left(b_{j}-l\right) \end{aligned}$$

1. 所得到的 $m_0, m_1, ….m_N$ 即为 target distribution 的 每个离散点 $z_0, z_1, …z_{N}$ 上的概率。这里由于是两个概率之间的差值，所以loss function采用cross-entropy ： $$-\sum_{i} m_{i} \log p_{i}\left(x_{t}, a_{t}\right)$$

至此，得到最终的算法：

附示意图一张：

Experiments

待补充

Discussion

待补充