[Paper][RL][ICML 2016] Dueling DQN

论文：[ICML 2016] Dueling Network Architectures for Deep Reinforcement Learning

引子

如果说Double DQN，Prioritized Replay 是在 算法上对DQN的改进，那Dueling Network就是在网络结构上对 DQN的改进。和DQN相比，只需要将DQN中的网络替换成Dueling Network，其他部分保持不变。

Why Dueling Network work?

1. Dueling Network将 $Q$ 的学习拆分为 $V$ 和 $A$ 的学习。不同于 Single Network中每次更新时只有对应action的参数得到了更新，在Dueling Network中，每次更新，$V$ 都得到了更新。$V$ 的学习非常充分，对 $true \ V$ 的拟合也就更好，所以Q-learning 这种 Temporal Difference(TD) 算法的效果也好。
2. 对于一个state，可能其 $Q(s,a)$ 的绝对大小较大，但是 $Q(s,a_1), Q(s,a_2)…$ 之间的相差并不大，论文中以 game Seaquest举了例子。如果直接学习 $Q$ ，可能Q的绝对大小学的大差不差，但是 $Q(s,a_1), Q(s,a_2)…$ 之间的大小关系并不容易学习。所以这里将大小关系单独提出来进行学习（即 Advantage Branch）

Algorithm

Dueling Network的网络结构如下，两个branch分别预测 $V(s)$ 和 $A(s,a)$：

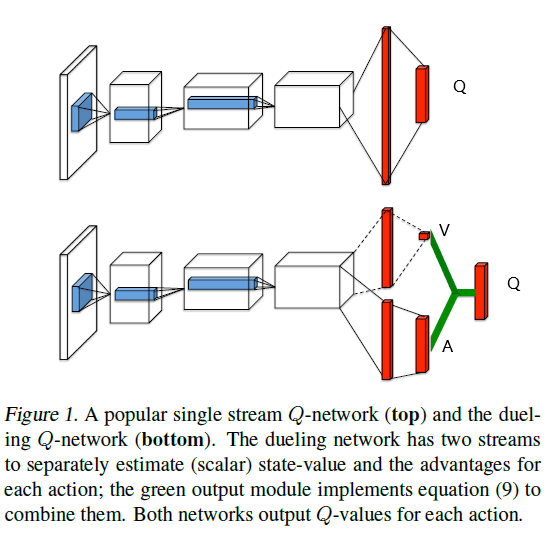
回忆 Advantage 的定义：$A(s,a) = Q(s,a) - V(s)$，似乎可以将Dueling Q-network的output layer构造成两个branch的简单相加：

$$Q(s, a ; \theta, \alpha, \beta)=V(s ; \theta, \beta)+A(s, a ; \theta, \alpha)$$

（注： $\theta$ 为共享卷积层的参数， $\alpha $ 为 branch A的参数， $\beta$ 为 branch V 的参数）

但是作者认为这样是没有意义的（lack of identifiability）。因为，一种最极端的情况是，branch V全部输出0，branch A输出Q，这就退化成了DQN。总的来说，branch V需要知道自己在approximate V，branch A也需要知道自己在approximate A。

作者也做了相关的实验，如果直接这么构造输出层，实际的结果很差。

于是，作者接下来提出了这样来构造output layer：

$$\begin{aligned} &Q(s, a ; \theta, \alpha, \beta)=V(s ; \theta, \beta)+ \left(A(s, a ; \theta, \alpha)-\max _{a^{\prime} \in|\mathcal{A}|} A\left(s, a^{\prime} ; \theta, \alpha\right)\right) \end{aligned}$$

当 $a = a^$ 时，显然上式中第二项 $ A(s, a ; \theta, \alpha)-\max _{a^{\prime} \in|\mathcal{A}|} A\left(s, a^{\prime} ; \theta, \alpha\right) $ 为0，于是branch V 需要 approximate $Q(s, a^ )$ 即 $V(s)$。

这样一来，branch V 就知道自己在approximate V了。既然branch V 知道自己在approximate V，这也使得了 branch A 知道自己在approximate A了。（这个地方有一点难以理解，反正最终work了）

不过，作者最终使用的是下面这个式子：

$$\begin{aligned} &Q(s, a ; \theta, \alpha, \beta)=V(s ; \theta, \beta)+\left(A(s, a ; \theta, \alpha)-\frac{1}{|\mathcal{A}|} \sum_{a^{\prime}} A\left(s, a^{\prime} ; \theta, \alpha\right)\right) \end{aligned}$$

它与之前那个式子没有本质上的区别，仅仅是为了提高训练的稳定性 [1] 。

Experiments

Policy Evaluation

Dueling DQN比DQN优越之处，就是在于 预测 $Q$ 比 single stream(DQN) 更准。 而如何比较谁的 $Q$ 更准，最直接的就是抛开 policy improvement， 比较谁的 Evaluation的结果更精确。

于是作者在一个toy environment(corridor) 做了实验。Dueling Network预测的 $Q$ 与 true $Q$ 相差更小，且收敛更快。当 #action 变大时，这个现象更明显。

Atari

在Atari上的结果如下；

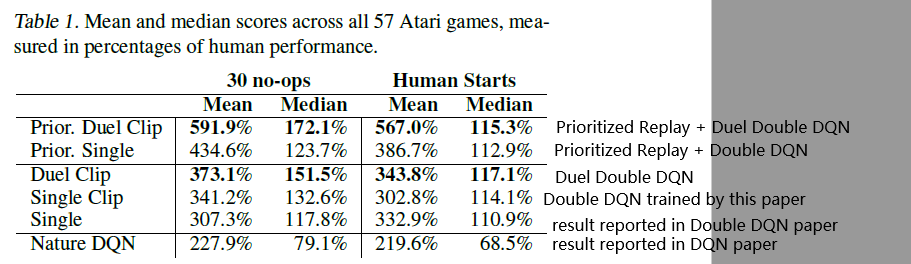
有几点值得注意的：

1. We clip the gradients to have their norm less than or equal to 10. 这篇论文发现 gradient clip 尤其的有效。比如表中 Single vs Single Clip，有不小的提升，所以对于所有模型几乎都使用了 Clip。
2. Prioritized Replay , Double Q-learning, Dueling Network 可以结合在一起，共同提升结果。

Saliency Map

Saliency Map有多种实现方式[2]。这里采取的是计算 Jacobian 矩阵。

参考资料

[1] Difficulty in understanding identifiability in the “Dueling Network Architectures for Deep Reinforcement Learning” paper

[2] 【强化学习 117】Saliency Map - 张楚珩的文章 - 知乎