[Paper][RL][AAAI 2016] Double DQN

强化学习

发布日期: 2021-07-31

更新日期: 2022-06-01

文章字数: 1k

阅读时长: 4 分

引子

这篇文章的创新之处并不多，可以用一句话概括：将 DQN 中的 Q-learning换成了 Double Q-learning。DQN算法和代码中需要修改的地方不超过2行。

所以，这篇文章基本没提算法，而是用大量篇幅描写各种实验，以展示Q-learning引入的bias，以及Double Q-learning 如何改善这种bias，进而改进policy。甚至，因为和DQN太像了，在论文中没有给出 Double DQN的算法伪代码。

不过，这篇论文图文并茂的解释了Q-learning所带来的overeestimation问题。之前看Sutton的书时，理解并不深刻，这篇论文却从多个角度让我加深了理解。

论文总结 & Motivation

这篇文章提出并解答了几个问题：

Q-learning(DQN) 是否存在 overestimation现象？存在。
overestimation是否一定会影响policy？如果uniformly overestimate，则不会。但大多数情况下并不是uniformly，所以会。
如何将Double Q-learning加到DQN中？非常简单的修改。
Double Q-learning(Double DQN) 是否缓解了overestimation，并使得最终得到的policy有了提升？是的。

注：overestimation是否只能通过Double learning解决？不一定，Rainbow[1]中认为 Distributional RL[2] 可以部分替代 Double Q-learning的作用

Algorithm

Double DQN相比DQN唯一不同的地方，就是target的计算方式。

DQN中 target 的计算公式为：

$Y_{t}^{\mathrm{DQN}} \equiv R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a ; \theta_{t}^{-}\right)$

套用Double Q-learning，将上式改写为：

$Y_{t}^{\text {DoubleDQN }} \equiv R_{t+1}+\gamma Q_{target}\left(S_{t+1}, \underset{a}{\operatorname{argmax}} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}\right), \boldsymbol{\theta}_{t}^{-}\right)$

Double DQN中，选择action由 $\theta_{t}$ 完成，计算Q由 $\theta_{t}^{-}$(target network) 完成。定期将 $\theta_{t}^{-}$拷贝到 $\theta_{t}^{-}$ 上，不需要像 Double Q-learning那样交替更新。

Experiments

Double DQN缓解了 Overestimation

Double DQN选取了一些Atari中的游戏，与DQN做了对比，结果在下图中。这幅图清楚的展示了Double Q-learning的优点：

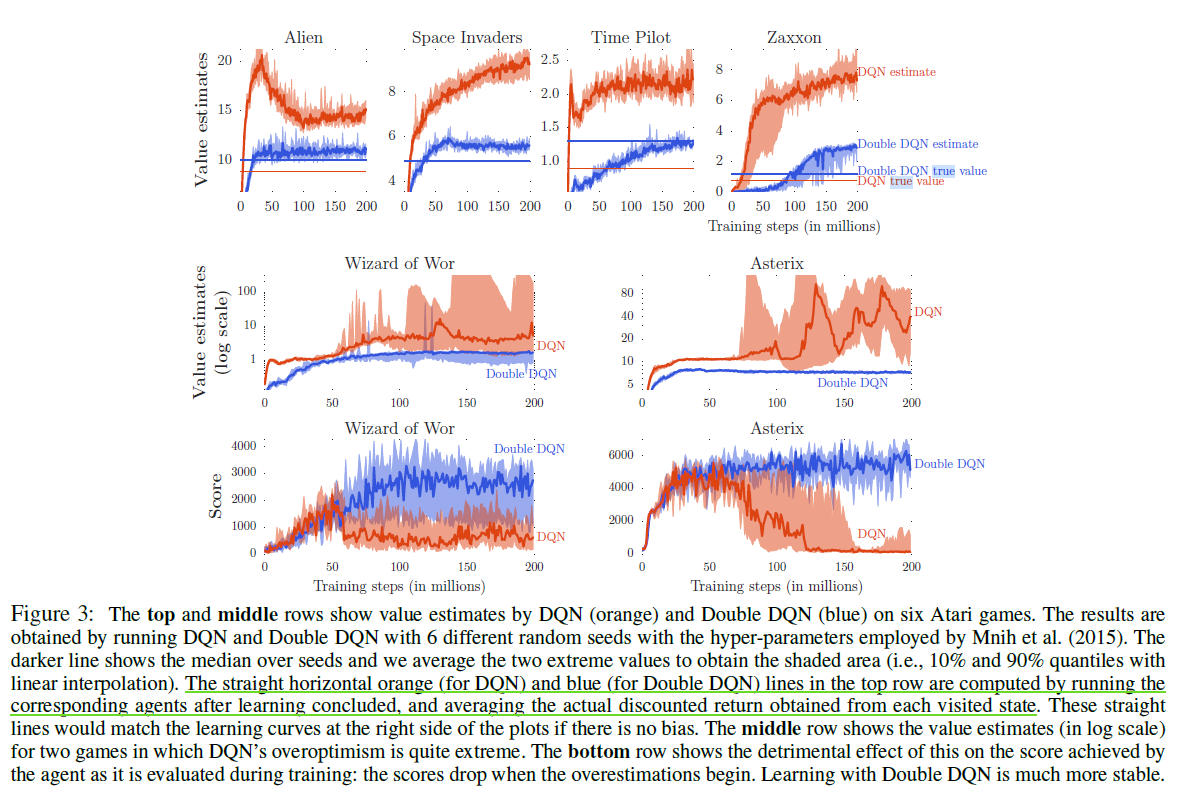
这幅图有几点需要解释的：

top row:

top row中的横线是 true value。指的是：当训练完成时，用训练好的网络，在某个state上，模拟多个episode，用episode的reward计算出真实的 $Q$ 值。所以，横线是 true Q of final policy。所以，需要关注的是训练完成时曲线与横线的差距。

显然训练完成时，Double DQN离true Double DQN更近一些，这说明Double DQN 的overestimation现象更不明显。
true Double DQN > true DQN。这说明 Double DQN 是比 DQN 更好的 policy（Q值的意义就是 expected reward）

middle & bottom row:

middle row是Atari中两种游戏的value estimate，注意到y轴是log scale的，这意味着value estimate与true Value相差非常之多。
middle row 中DQN在50 millons step时上涨明显，此时bottom row中scores中的DQN的曲线开始急速下降，论文中认为这并不是一种巧合。这说明overestimation确实对scores有坏的影响。
尽管这里只展示了2种游戏，但上述现象在Atari 中的所有游戏中都发生了，这可以证明 “在DQN中，overestimation对scores有坏的影响” 是一个普遍的结论

Double DQN 提高了 scores

文中分了两小节说明 Double DQN在 Atari上 1）仅就score而言，表现比 DQN要好 2）在human start上，泛化能力也更强。

Part 1 Quality of the learned policies

Part 1按照DQN的evaluton流程，starting point是通过no-op操作生成的，存在一定的随机性，但是随机性有限。

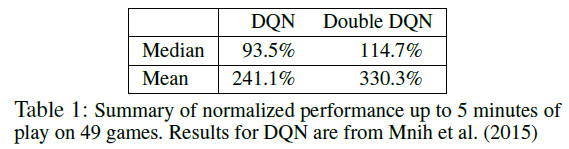
（注：表中Double DQN所用的超参与DQN保持一致，并没有调过。）

Part 2 Robustness to Human starts

Part 2 obtained 100 starting points sampled for each game from a human expert’s trajectory, as proposed by Nair et al. We start an evaluation episode from each of these starting points and run the emulator for up to 108,000 frames.

与Part 1相比，Part 2 的starting points更为随机，更考验模型的泛化能力。实验结果也佐证了这一点，DQN、Double DQN均有下滑。