[Paper][RL][ICLR 2016] Prioritized Experience Replay

论文地址：ICLR 2016 Prioritized Experience Replay

引子

本篇论文是DQN中Experience Replay的后续工作。

Motivation

The key idea is that an RL agent can learn more effectively from some transitions than from others.

Example: Blind Cliffwalk

论文中用了一个例子来说明不同样本需要不同权重的必要性。

在下图中的 Cliffwalk中，显然，agent只有 $1/2^{n-1}$ 的概率到达终点，所以，replay memory中有大量的雷同的transition，只有极少数到达终点的episode的transition。而这些极少数的transition相对而言更加重要。

（注：这个example的详细setup可以在 Appendix中找到。 由于Cliffwalk的可能的episode个数是有限的，所以replay memory不会进行淘汰，包含了所有可能的episode的transition。对于 n 个 state的Cliffwalk来说，可能的transition个数为 $2^{n+1} - 2$，成功到达终点的transition个数为 $n-1$，如果均匀抽样，选中的概率可以说是非常小了）

下图右展示了最优抽样（oracle)和均匀抽样情况下，Q函数收敛所需update次数与 cliffwalk中state[注1]的个数的关系。显然，两者有数量级的差异。图中折线是多次实验的中位数。

（注1：图中用的是#samples，和#states是等价的，成正比关系，#samples = $2^{n+1} - 2$ , n = #states）

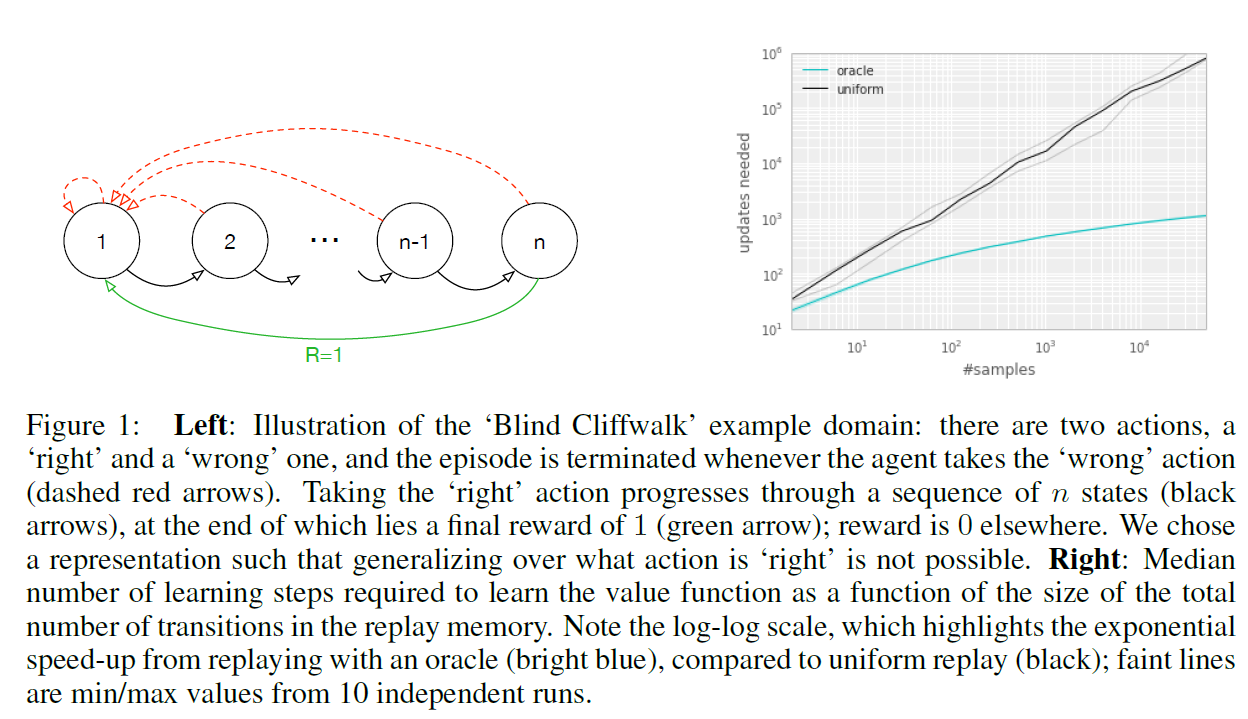
尽管这是个非常极端的例子，也某种程度上说明了 Prioritized Experience Replay 的重要性。

Algorithm

Prioritizing with TD error

这篇论文的核心问题为 如何estimate一个transition的重要性？这时候，可能有人会想到用另一个神经网络来estimate。且慢，有更简单的方法：

One idealised criterion would be the amount the RL agent can learn from a transition in its current state (expected learning progress).

而 the amount the RL agent can learn from a transition 用 TD error 来衡量。$\delta$ 越大，说明 loss 越大，$Q$ network 估计的越不准，被选中的优先级越高。

Stocastic Prioritization

只使用 $\delta$ 作为priority，根据 $\delta$ 的大小逐个选取transition 会产生了一系列的问题。比如：

• TD-error要实时更新。可能一开始某个transition的 $\delta$ 很低，但后来$\delta$ 变得很高。如果不实时更新，该transition的优先级一直都很低，永远得不到更新。

  然而，Replay memory 的数量级在 $10^6$ ，不可能做到实时更新。$\delta$ 只在transition被放入memory时 或 再次被放入时的 $\delta$ 才更新。

• 一些其他问题，参见论文。

基于以上问题，不能只根据 $\delta$ 来抽取样本，而是要随机一点。每个transition 被选中的概率：

$$\begin{equation} P(i)=\frac{p_{i}^{\alpha}}{\sum_{k} p_{k}^{\alpha}} \end{equation}$$

其中 $\alpha$ 为超参，在Atari 2600中设为 0.6 / 0.7。$p_k$ 为 priority，有两种不同的选择，这两种选择的performance互有好坏，需要按照情况选择。

1. Proportional Prioritization : $p_{i}=\left|\delta_{i}\right|+\epsilon$ ，其中 $\epsilon$ 的作用是使 $p_i > 0$
2. Rank-based Prioritization : $p_{i}=\frac{1}{\operatorname{rank}(i)}$ rank(i) 为 按照 $\left|\delta_{i}\right|$ 从大到小排序的序号。

看上去 Rank-based Prioritization 的效果应该会更好，但实际上不是，在Discussion部分作者解释为：

we expected the rank-based variant to be more robust because it is not affected by outliers nor error magnitudes. Furthermore, its heavy-tail property also guarantees that samples will be diverse, and the stratified sampling from partitions of different errors will keep the total minibatch gradient at a stable magnitude throughout training.

Perhaps surprisingly, both variants perform similarly in practice; we suspect this is due to the heavy use of clipping (of rewards and TD-errors) in the DQN algorithm, which removes outliers.

上述两者都是 $\left|\delta_{i}\right|$ 越大，$p_i$ 越大。只不过作者认为第二种更robust一点。

Importance Sampling

当我们根据Stocastic Prioritization来采样transition时，high priority的transition会被采样许多次，而low priority的transition会被采样较少的次数。用数学语言来说就是，原本我们uniformly 采样，求得 $\mathbb{E_{\sim uniform}[gradient]}$ ，现在换了一个分布采样，显然会引入bias。

（一个比较容易理解的例子是利用蒙特卡洛积分求曲线下面积，也引入了Importance Sampling修正bias，否则算出的曲线下面积是错误的）

为了修正这点，引入了Importance Sampling：

$$\begin{equation} w_{i}=\left(\frac{1}{N} \cdot \frac{1}{P(i)}\right)^{\beta} \end{equation}$$

当 $\beta = 1$ 时，bias完全被修正了。

在论文中采取的是逐步增大 $\beta$ 的操作，从 $\beta = \beta_0$ 逐步增大到 $\beta = 1$ 。

Algorithm: Double DQN with proportional prioritization

论文结合当时的SOTA Double DQN给出了最终的算法，红框中为与 Double DQN 不同的地方 ：

Experiment

实验的细节、参数基本和 DQN一致，这里不再赘述，只讲几点比较值得注意的：

1. memory 的淘汰方式并不是淘汰 $P(i)$ 最低的，仍然是淘汰最先进入memory的。
2. 超参 $\alpha$ = 0.7, $\beta_0$ = 0.5 （只有 $\beta$ 有 annealing）

1. Normalized Score

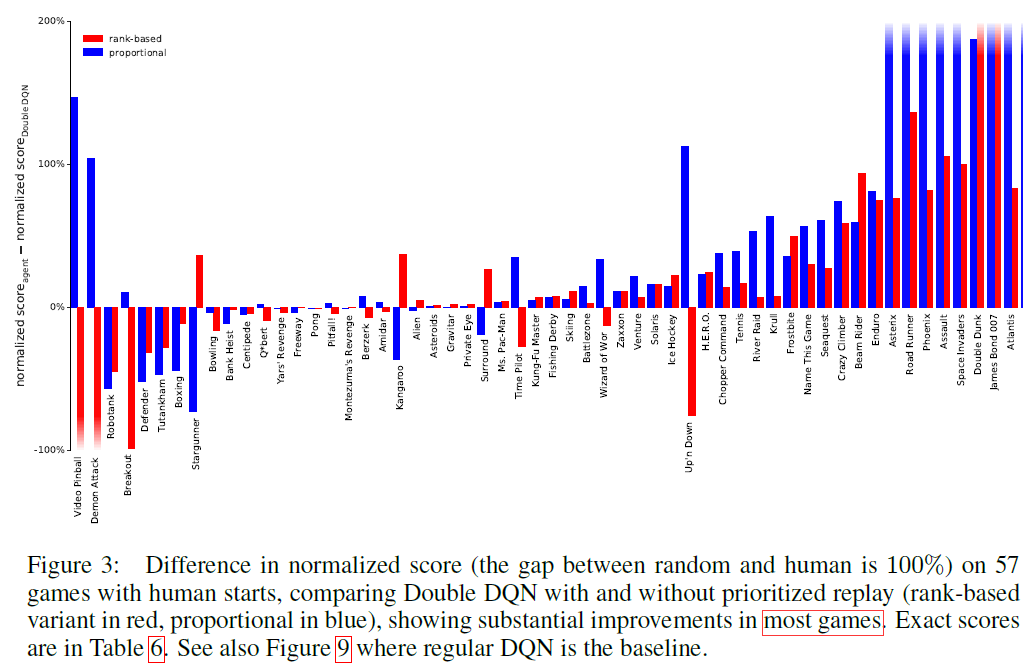
2. Learning speed

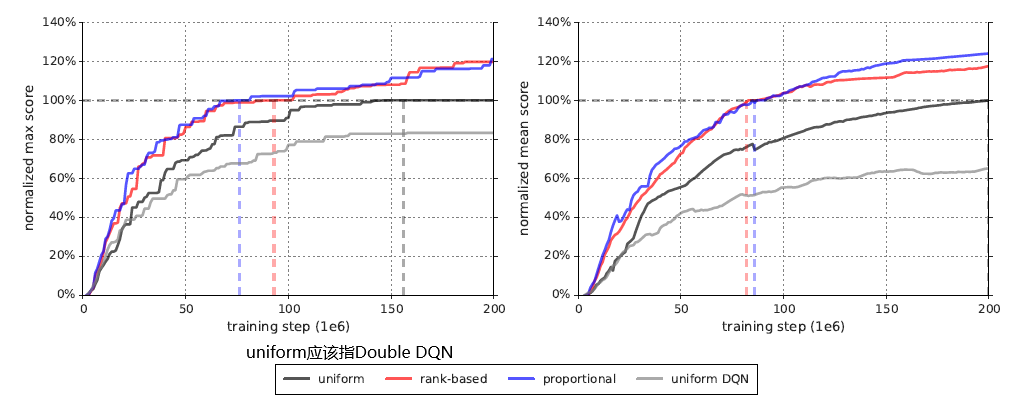
Discussion

待补充

Extension

Prioritized Supervised Learning：一般在 Supervised Learning中，由于我们知道各个类的数据量，对于unbalanced的dataset，一般是对数据量少的那一类做data augmentation，使得不同类的数据量持平。不过，假如我们不知道各个类的数据量呢？这篇论文将 Prioritized sampling ( $\alpha$ = 0.7, $\beta$ = 0，no annealing）应用在imbalanced MNIST上：

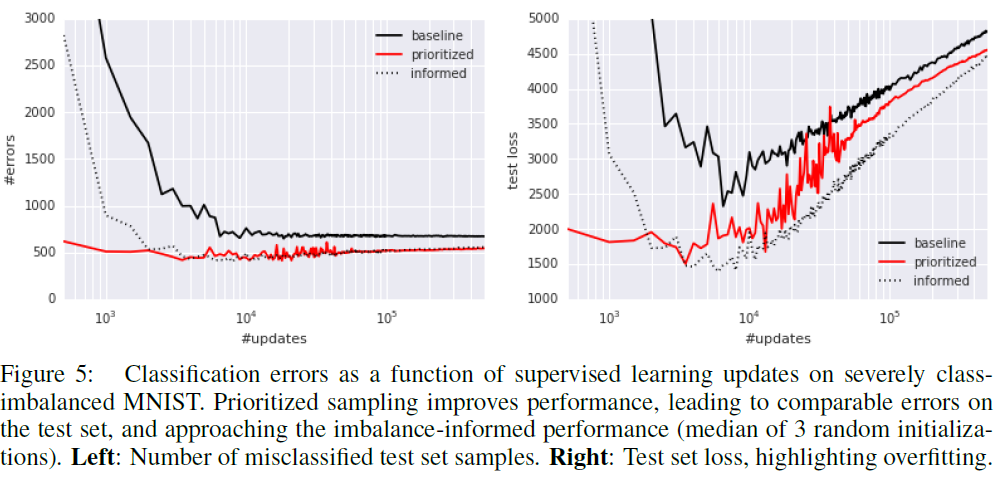
参考资料

[1] Prioritized-replay-what-does-importance-sampling-really-do